Question

Suppose that a random sample of 16 measures from a normally distributed population gives a sample mean of x=13.5 and a sample standard deviation of s=6. the null hypothesis is equal to 15 and the alternative hypothesis is not equal to 15. using hypothesis testing for t values do you reject the null hypothesis at alpha=.10 level of significance?

Answer 1

Explanation:

The summary of the statistics given include:

population mean
`\mu` = 15

sample mean
`\oerline x` = 13.5

sample size n = 16

standard deviation s = 6

The level of significance ∝ = 0.10

The null and the alternative hypothesis can be computed as follows:

`\mathtt{H_o: \mu = 15} \\ \\ \mathtt{H_1 : \mu \\eq 15}`

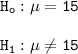
Since this test is two tailed, the t- test can be calculated by using the formula:

`t = (\overline x - \mu)/((\sigma )/(√(n)))`

`t = (13.5 - 15)/((6)/(√(16)))`

`t = (- 1.5)/((6)/(4))`

`t = (- 1.5* 4)/(6)}`

`t = (- 6.0)/(6)}`

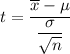
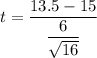
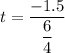
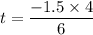
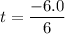
t = - 1

degree of freedom = n - 1

degree of freedom = 16 - 1

degree of freedom = 15

From the standard normal t probability distribution table, the p value when t = -1 at 0.10 level of significance, the p - value = 0.3332

Decision Rule: We fail to reject the null hypothesis since the p-value is greater than the level of significance at 0.10

Conclusion: Therefore, we can conclude that there is insufficient evidence at the 0.10 level of significance to conclude that the population mean μ is different than 15.