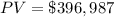Answer:
The present value is
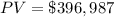
Explanation:
From the question we are told that
The interest payment per year is
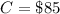
The principal payment is
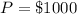
The duration is n = 8 years
The interest rate is
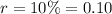
The present value is mathematically represented as
![PV = [ (C)/(r) * [1 - (1 )/( (1 +r)^n) ] + (P)/((1 + r)^n) ]](https://img.qammunity.org/2021/formulas/mathematics/college/t8hkud8fase95jrpcrf9ao4t01djru8xsg.png)
substituting values
![PV = [ (85)/(0.10) * [1 - (1 )/( (1 +0.10)^8) ] + (1000)/((1 + 0.10)^ 8) ]](https://img.qammunity.org/2021/formulas/mathematics/college/hm4q0a10unku9yudeszdae1cj4fwlsobdb.png)