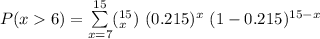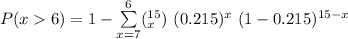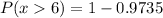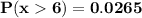Question

A baseball player has a batting average (probability of getting on base per time at bat) of 0.215. Based on this: What is the probability that they will get on base more than 6 of the next 15 at bats

Answer 1

`\mathbf{P(x>6) = 0.0265}`

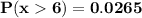
Explanation:

Given that:

A baseball player has a batting average (probability of getting on base per time at bat) of 0.215

i.e

let x to be the random variable,

consider
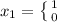`x_1 = \left \{ {{1} \atop {0}} \right.` to be if the baseball player has a batting average or otherwise.

Then

p(x₁ = 1) = 0.125

What is the probability that they will get on base more than 6 of the next 15 at bats

So

`\mathtt{x_i \sim Binomial (n,p)}`

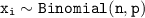
where; n = 15 and p = 0.125

P(x>6) = P(x ≥ 7)

`P(x>6) = \sum \limits ^(15)_(x=7) ( ^(15 )_x ) \ (0.215)^x \ (1 - 0.215)^(15-x)`

`P(x>6) = 1 - \sum \limits ^(6)_(x=7) ( ^(15 )_x ) \ (0.215)^x \ (1 - 0.215)^(15-x)`

`P(x>6) = 1 - \sum \limits ^(6)_(x=0) ( ^(15 )_x ) \ (0.215)^x \ (1 - 0.215)^(15-x)`

`P(x>6) = 1 -0.9735`

`\mathbf{P(x>6) = 0.0265}`