Question

A researcher at the University of Washington medical school believes that energy drink consumption may increase heart rate. Suppose it is known that heart rate (in beats per minute) is normally distributed with an average of 70 bpm for adults. A random sample of 25 adults was selected and it was found that their average heartbeat was 73 bpm after energy drink consumption, with a standard deviation of 7 bpm. In order to test belief at the 10% significance level, determine P-value for the test.

Answer 1

Explanation:

Given that:

mean μ = 70

sample size = 25

sample mean = 73

standard deviation = 7

level of significance = 0.10

The null hypothesis and the alternative hypothesis can be computed as follows:

`\mathtt{H_o : \mu = 70} \\ \\ \mathtt{H_1 : \mu > 70 }`

The z score for this statistics can be calculated by using the formula:

`z = (X- \mu)/((\sigma)/(√(n)))`

`z = (73- 70)/((7)/(√(25)))`

`z = (3)/((7)/(5))`

`z = \frac{3 * 5}{{7}{}}`

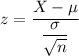
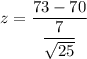
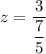
z = 2.143

At level of significance of 0.10

degree of freedom = n -1

degree of freedom = 25 - 1

degree of freedom = 24

The p - value from the z score at level of significance of 0.10 and degree of freedom of 24 is:

P - value = 1 - (Z < 2.143)

P - value = 1 - 0.9839

P - value = 0.0161

Decision Rule: since P value is lesser than the level of significance, we reject the null hypothesis.

Conclusion: We conclude that energy drink consumption increases heart rate.