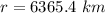Question

The ancient Greek Eratosthenes found that the Sun casts different lengths of shadow at different points on Earth. There were no shadows at midday in Aswan as the Sun was directly overhead. 800 kilometers north, in Alexandria, shadow lengths were found to show the Sun at 7.2 degrees from overhead at midday. Use these measurements to calculate the radius of Earth.

Answer 1

The radius of the earth is
`r = 6365.4 \ km`

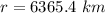
Step-by-step explanation:

From the question we are told that

The distance at Alexandria is
`d_a = 800 \ km = 800 *10^(3) \ m`

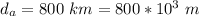
The angle of the sun is
`\theta = 7.2 ^o`

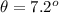
So we want to first obtain the circumference of the earth

So let assume that the earth is circular (
`360 ^o`)

Now from question we know that the sun made an angle of
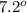`7.2 ^o` so with this we will obtain how many
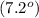`(7.2 ^o)` are in
`360^o`

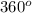
i.e
`N = (360)/(7.2)`

=>
`N = 50`

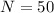
With this value we can evaluate the circumference as

`c = 50 * 800`

`c = 40000 \ km`

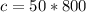
Generally circumference is mathematically represented as

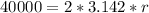
`c = 2\pi r`

`40000 = 2 * 3.142 * r`

=>
`r = 6365.4 \ km`