Question

PLS HELP!! Consider the exponential functions f, g, and h, defined as shown. Determine which function or functions have each key feature. Drag the tiles to the correct boxes. Not all tiles will be used.

Answer 1

A) f(x) and g(x)

B) only g(x)

C) All three functions

D) f(x) and h(x)

Explanation:

In my uploaded image on the test I have gotten C) wrong but if you graph all three functions, you can see that all three functions have the same style of -∞

end behavior so I think that would be the most logical answer.

Answer 2

The function or functions should be matched to each correct key feature as follows;

increasing on all intervals of x ↔ only g(x).

approaches an integer as x approaches -∞ ↔ all three functions.

y-intercept at (0, 4) ↔ f(x) and g(x)

x-intercept at (1, 0) ↔ f(x) and h(x)

For any given function, y = f(x), if the output value is increasing when the input value is increased, then, the function is generally referred to as an increasing function.

Based on the information provided above, we can logically deduce that only the exponential function g(x) is increasing on all intervals of x.

The end behavior of all exponential three functions is that as x approaches negative infinity (-∞), they approache an integer;

`\lim_(x \to -\infty) f(x), \;g(x),\;and\;g(x) =integer`

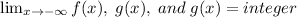
The intercept of a graph is the point where the graph of a line crosses either the x-axis or the y-axis on a coordinate plane. Based on three exponential functions, the correct intercepts are as follows;

x-intercept of f(x) and h(x)= (1, 0)

y-intercept of f(x) and g(x) = (0, -2)