Question

A conveyor belt carries supplies from the first floor to the second floor, which is 21 feet higher. The belt makes a 60° angle with the ground. How far do the supplies travel from one end of the conveyor belt to the other? Round your answer to the nearest foot. If the belt moves at 75 ft/min, how long, to the nearest tenth of a minute, does it take the supplies to move to the second floor?

Answer 1

Hey there! I'm happy to help!

LENGTH OF CONVEYOR BELT

We are going to have to use some trigonometry. Let's think of this as a right triangle. The conveyor belt is the diagonal or the hypotenuse, while the ground is and the height of the room make a right angle as the legs.

We have a sixty degree angle between the conveyor belt and the ground. This is means that the 21 foot height is the opposite side of our right triangle. So, we are dealing with the opposite and the hypotenuse, so we will use the sine. The sine of an angle is equal to the opposite length divided by the hypotenuse length.

We will set up the following equation and solve for the length of our conveyor belt (c).

`sin60=(21)/(c)`

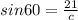
We multiply both sides by c.

`c(sin60)=21`

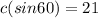
We divide both sides by sin60.

`c=(21)/(sin60)`

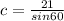
If we evaluate this with a calculator, we get that c is equal to 24.2487113..., or 24 when rounded to the nearest foot.

So, the supplies travel 24 feet from one end to the other.

DURATION OF TRAVEL

We want to find how long it takes the supplies to move across the conveyor belt. We see that every minute, it moves 75 feet. We want to see how many minutes it will take to move 24 feet, as that is the length of the conveyor belt as we previously solved. Let's set up a proportion.

`(feet)/(minute) =(75)/(1) =(24)/(m)`

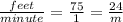
We cross multiply, giving us the following equation.

75m=24

We divide both sides by 75.

m=0.32

We want to round to the nearest tenth of a minute, so it will take 0.3 minutes for the supplies to move to the second floor.

Have a wonderful day! :D