Final answer:
The model for the sales of the Garland Corporation between 2010 and 2015 is:

Step-by-step explanation:
To find a model for the sales of the Garland Corporation between 2010 and 2015, we can use the exponential growth formula:
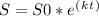
where S is the sales in year t, S0 is the initial sales in year 2010, e is the base of the natural logarithm (approximately 2.71828), k is the growth rate, and t represents the number of years.
Given that the sales in 2010 (t = 0) are $110 million (S0 = 110), and the sales in 2015 (t = 5) are projected to be $160 million (S = 160), we can substitute these values into the formula:

To solve for k, we can divide both sides of the equation by 110 and then take the natural logarithm of both sides:
ln(160/110) = 5k
Now we can divide both sides by 5 to isolate k:
k = ln(160/110)/5
Calculating this value, we get:
k ≈ 0.0845 (rounded to four decimal places)
Therefore, the model for the sales of the Garland Corporation between 2010 and 2015 is:

This equation gives the sales of the company in year t, where t represents the number of years between 2010 and 2015.
Your question is incomplete, but most probably the full question was:
The sales of the Garland Corporation are projected to grow exponentially for the years between 2010 and 2015 from $110 million to $160 million.
Find a model giving the sales of Garland Corporation in year t between 2010 (t = 0) and 2015 (t = 5).
Hint: The sales in year t are S = S0ekt.(Round your value of k to four decimal places.)
S(t)