Question

A 51-foot wire running from the top of a tent pole to the ground makes an angle of 58° with the ground. If the length of the tent pole is 44 feet, how far is it from the bottom of the tent pole to the point where the wire is fastened to the ground? (The tent pole is not necessarily perpendicular to the ground.)

Answer 1

35.11 ft

Explanation:

This given situation can be thought of as triangle
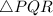`\triangle PQR` where PQ is the length of pole.

PR is the length of rope.

and QR is the distance of bottom of pole to the point of fastening of rope to the ground.

And
`\angle Q \\eq 90^\circ`

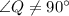
Given that:

PQ = 44 ft

PR = 51 ft

`\angle R = 58^\circ`

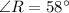
To find:

Side QR = ?

Solution:

We can apply Sine Rule here to find the unknown side.

Sine Rule:

`(a)/(sinA) = (b)/(sinB) = (c)/(sinC)`

Where

a is the side opposite to
`\angle A`

b is the side opposite to
`\angle B`

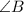
c is the side opposite to
`\angle C`

`(PR)/(sinQ)=(PQ)/(sinR)\\\Rightarrow sin Q =(PR)/(PQ)* sinR\\\Rightarrow sin Q =(51)/(44)* sin58^\circ\\\Rightarrow \angle Q =79.41^\circ`

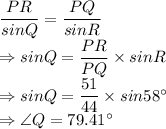
Now,

`\angle P +\angle Q +\angle R =180^\circ\\\Rightarrow \angle P +58^\circ+79.41^\circ=180^\circ\\\Rightarrow \angle P = 42.59^\circ`

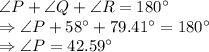
Let us use the Sine rule again:

`(QR)/(sinP)=(PQ)/(sinR)\\\Rightarrow QR =(sinP)/(sinR)* PQ\\\Rightarrow QR =(sin42.59)/(sin58)* 44\\\Rightarrow QR = 35.11\ ft`

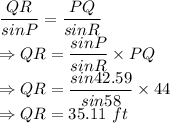
So, the answer is 35.11 ft.