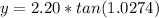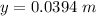How wide is the central diffraction peak on a screen 2.20 mm behind a 0.0328-mmmm-wide slit illuminated by 588-nmnm light?

Question

asked Feb 13, 2021 97.2k views

1 Answer

Beno Odr · Answer 1 · 2021-02-19T21:26:28+0000

Answer:

$y = 0.0394 \ m$

Step-by-step explanation:

From the question we are told that

The distance of the screen is
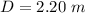
$D = 2.20 \ m$

The distance of separation of the slit is
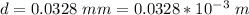
$d = 0.0328 \ mm = 0.0328*10^(-3) \ m$

The wavelength of light is
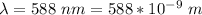
$\lambda = 588 \ nm = 588 *10^(-9) \ m$

Generally the condition for constructive interference is

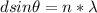
$dsin\theta = n * \lambda$

=>
$\theta = sin^(-1) [ ( n * \lambda )/(d ) ]$

here n = 1 because we are considering the central diffraction peak

=>
$\theta = sin^(-1) [ ( 1 * 588*10^(-9) )/(0.0328*10^(-3) ) ]$

=>
$\theta = 1.0274 ^o$

Generally the width of central diffraction peak on a screen is mathematically evaluated as

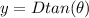
$y = D tan (\theta )$

substituting values

y = 2.20 * tan (1.0274)

$y = 0.0394 \ m$