Question

According to the Census Bureau, 3.34 people reside in the typical American household. A sample of 26 households in Arizona retirement communities showed the mean number of residents per household was 2.70 residents. The standard deviation of this sample was 1.17 residents. At the .10 significance level, is it reasonable to conclude the mean number of residents in the retirement community household is less than 3.34 persons?

(a) State the null hypothesis and the alternate hypothesis. (Round your answer to 2 decimal places.)


H0: ? ?
H1: ? <


(b)
State the decision rule for .10 significance level. (Negative amount should be indicated by a minus sign. Round your answer to 3 decimal places.)



Reject H0 if t <

(c)
Compute the value of the test statistic. (Negative amount should be indicated by a minus sign. Round your answer to 3 decimal places.)



Value of the test statistic

(d)
Is it reasonable to conclude the mean number of residents in the retirement community household is less than 3.34 persons?



H0. Mean number of residents less than 3.34 persons.

Answer 1

Explanation:

Given that:

Mean = 3.34

sample size = 26

sample mean = 2.7

standard deviation = 1.17

level of significance = 0.10

The null hypothesis and the alternative hypothesis can be computed as follows:

`\mathtt{H_o: \mu \geq 3.34} \\ \\ \mathtt{H_1: \mu < 3.34}`

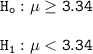
degree of freedom = n - 1

degree of freedom = 26 -1

degree of freedom = 25

level of significance = 0.10

Since the alternative hypothesis contains <, then the test is left tailed

`\mathtt{t_(\alpha, df) = t_(0.10, 25)}`

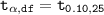
`\mathtt{t_(0.10, 25)}` = - 1.316

The rejection region therefore consist of all values smaller than - 1.316, therefore ; reject
`H_o` if t < -1.316

The test statistics can be computed as follows:

`t = (X - \mu)/((\sigma)/(√(n)))`

`t = (2.7 - 3.34)/((1.17)/(√(26)))`

`t = (-0.64)/((1.17)/(5.099))`

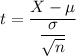
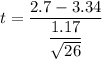
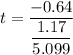
t = - 2.789

Decision Rule: To reject the null hypothesis if the t test lies in the rejection region or less than the rejection region.

Conclusion: We reject the null hypothesis since t = (- 2.789) < -1.316. Then we conclude that the mean number of residents in the retirement community household is less than 3.34 persons.