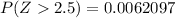Question

If the average yield of cucumber acre is 800 kg, with a variance 1600 kg, and that the amount of the cucumber follows the normal distribution. 1- What percentage of a cucumber give the crop amount between 778 and 834 kg? 2- What the probability of cucumber give the crop exceed 900 kg ?

Answer 1

a

The percentage is

`P(x_1 < X < x_2 ) = 51.1 \%`

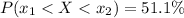
b

The probability is
`P(Z > 2.5 ) = 0.0062097`

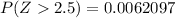
Explanation:

From the question we are told that

The population mean is
`\mu = 800`

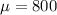
The variance is
`var(x) = 1600 \ kg`

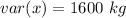
The range consider is
`x_1 = 778 \ kg \ x_2 = 834 \ kg`

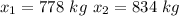
The value consider in second question is
`x = 900 \ kg`

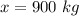
Generally the standard deviation is mathematically represented as

`\sigma = √(var (x))`

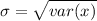
substituting value

`\sigma = √(1600)`

`\sigma = 40`

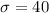
The percentage of a cucumber give the crop amount between 778 and 834 kg is mathematically represented as

`P(x_1 < X < x_2 ) = P( (x_1 - \mu )/(\sigma) < (X - \mu )/( \sigma ) < (x_2 - \mu )/(\sigma ) )`

Generally
`(X - \mu )/( \sigma ) = Z (standardized \ value \ of \ X)`

So

`P(x_1 < X < x_2 ) = P( (778 - 800 )/(40) < Z< (834 - 800 )/(40 ) )`

`P(x_1 < X < x_2 ) = P(z_2 < 0.85) - P(z_1 < -0.55)`

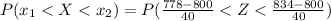
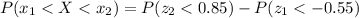
From the z-table the value for
`P(z_1 < 0.85) = 0.80234`

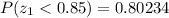
and
`P(z_1 < -0.55) = 0.29116`

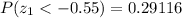
So

`P(x_1 < X < x_2 ) = 0.80234 - 0.29116`

`P(x_1 < X < x_2 ) = 0.51118`

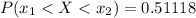
The percentage is

`P(x_1 < X < x_2 ) = 51.1 \%`

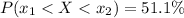
The probability of cucumber give the crop exceed 900 kg is mathematically represented as

`P(X > x ) = P((X - \mu )/(\sigma ) > (x - \mu )/(\sigma ) )`

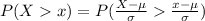
substituting values

`P(X > x ) = P( (X - \mu )/(\sigma ) >(900 - 800 )/(40 ) )`

`P(X > x ) = P(Z >2.5 )`

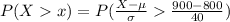
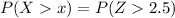
From the z-table the value for
`P(Z > 2.5 ) = 0.0062097`