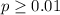Question

It is advertised that the average braking distance for a small car traveling at 65 miles per hour equals 122 feet. A transportation researcher wants to determine if the statement made in the advertisement is false. She randomly test drives 38 small cars at 65 miles per hour and records the braking distance. The sample average braking distance is computed as 116 feet. Assume that the population standard deviation is 21 feet. (You may find it useful to reference the appropriate table: z table or t table) a. State the null and the alternative hypotheses for the test.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

the null hypothesis is
`H_o : \mu = 122`

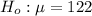
the alternative hypothesis is
`H_a : \mu \\e 122`

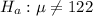
The test statistics is
`t = - 1.761`

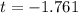
The p-value is
`p = P(Z < t ) = 0.039119`

so

`p \ge 0.01`

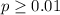
Explanation:

From the question we are told that

The population mean is
`\mu = 122`

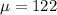
The sample size is n= 38

The sample mean is
`\= x = 116 \ feet`

The standard deviation is
`\sigma = 21`

Generally the null hypothesis is
`H_o : \mu = 122`

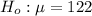
the alternative hypothesis is
`H_a : \mu \\e 122`

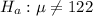
Generally the test statistics is mathematically evaluated as

`t = \frac { \= x - \mu }{( \sigma )/( √(n) ) }`

substituting values

`t = \frac { 116 - 122 }{( 21 )/( √( 38) ) }`

`t = - 1.761`

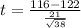
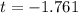
The p-value is mathematically represented as

`p = P(Z < t )`

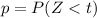
From the z- table

`p = P(Z < t ) = 0.039119`

So

`p \ge 0.01`