Question

A thin film of soap with n = 1.37 hanging in the air reflects dominantly red light with λ = 696 nm. What is the minimum thickness of the film?

Answer 1

The thickness is
`t = 1.273 *10^(-7) \ m`

Step-by-step explanation:

From the question we are told that

The refractive index of the film is
`n = 1.37`

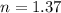
The wavelength is
`\lambda = 696 \ nm = 696 *10^(-9 ) \ m`

Generally the condition for constructive interference in a film is mathematically represented as

`2 * t = [m + (1)/(2) ] \lambda_k`

Here t is the thickness of the film , m is the order number (0, 1, 2, 3 ... )

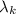`\lambda _k` is the wavelength of light that is inside the film , this is mathematically evaluated as

`\lambda _k = ( \lambda )/( n)`

`\lambda _k = ( 696 *10^(-9))/( 1.37)`

`\lambda _k = 5.095 *10^(-7 ) \ m`

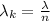
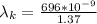
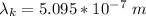
So for m = 0

`t = [ 0 + (1)/(2) ] \lambda _k * (1)/(2)`

substituting values

`t = [ 0 + (1)/(2) ] (5.095 *10^(-7)) * (1)/(2)`

`t = 1.273 *10^(-7) \ m`