Question

What is the tangent ratio of KJL? (Question and answers provided in picture.)

Answer 1

option A

Explanation:

Answer 2

Option (1)

Explanation:

The given triangle JKL is an equilateral triangle.

Therefore, all three sides of this triangle will be equal in measure.

Side JK = JL = KL = 48 units

Perpendicular LM drawn to the base JK bisects the base in two equal parts JM and MK.

By applying tangent rule in ΔJML,

tan(∠KJL) =
`\frac{\text{Opposite side}}{\text{Adjacent side}}`

=
`\frac{\text{LM}}{\text{JM}}`

=
`\frac{\text{LM}}{24}`

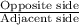
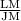
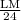
Since, Sin(K) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

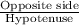
Sin(60)° =
`\frac{\text{LM}}{48}`

`(√(3))/(2)=\frac{\text{LM}}{48}`

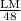
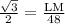
LM = 24√3

Now, tan(∠KJL) =
`\frac{\text{LM}}{24}`

=
`(24√(3) )/(24)`

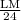
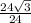
Therefore, Option (1) will be the answer.