Question

Using a table of values, determine the solution to the equation below to the nearest fourth of a unit. 2^x=1-3^x

Answer 1

Option (1)

Explanation:

Given equation is,

`2^x=1-3^x`

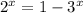
To determine the solution of the equation we will substitute the values of 'x' given in the options,

Option (1)

For x = -0.75

`2^(-0.75)=1-3^(-0.75)`

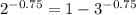
0.59 = 1 - 0.44

0.59 = 0.56

Since, values on both the sides are approximately same.

Therefore, x = -0.75 will be the answer.

Option (2)

For x = -1.25

`2^(-1.25)=1-3^(-1.25)`

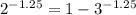
0.42 = 1 - 0.25

0.42 = 0.75

Which is not true.

Therefore, x = -1.25 is not the answer.

Option (3)

For x = 0.75

`2^(0.75)=1-3^(0.75)`

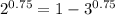
1.68 = 1 - 2.28

1.68 = -1.28

Which is not true.

Therefore, x = 0.75 is not the answer.

Option (4)

For x = 1.25

`2^(1.25)=1-3^(1.25)`

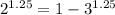
2.38 = 1 - 3.95

2.38 = -2.95

It's not true.

Therefore, x = 1.25 is not the answer.