Question

On a coordinate plane, a line has points (negative 2, negative 4) and (4, 2). Point P is at (0, 4). Which points lie on the line that passes through point P and is parallel to the given line? Select three options. (–4, 2) (–1, 3) (–2, 2) (4, 2) (–5, –1)

Answer 1

b,c,e

Explanation:

I got it right on edge

Answer 2

the correct options are:

(–1, 3), (–2, 2) and (–5, –1)

Explanation:

Given that a line passes through two points

A(-2, -4) and B(4, 2)

Another point P(0, 4)

To find:

Which points lie on the line that passes through P and is parallel to line AB ?

Solution:

First of all, let us the find the equation of the line which is parallel to AB and passes through point P.

Parallel lines have the same slope.

Slope of a line is given as:

`m=(y_2-y_1)/(x_2-x_1)`

`m=(2-(-4))/(4-(-2)) = 1`

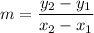
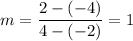
Now, using slope intercept form (
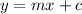`y = mx+c`) of a line, we can write the equation of line parallel to AB:

`y =(1)x+c \Rightarrow y = x+c`

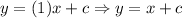
Now, putting the point P(0,4) to find c:

`4 = 0 +c \Rightarrow c = 4`

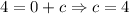
So, the equation is
`\bold{y=x+4}`

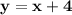
So, the coordinates given in the options which have value of y coordinate equal to 4 greater than x coordinate will be true.

So, the correct options are:

(–1, 3), (–2, 2) and (–5, –1)