Question

If triangle ABC, m B = 90°, cos(9 = 17, and AB = 16 units.

Based on this information, m Note that the angle measures are rounded to the nearest degree.
units.

Answer 1

m∠A = 62°

m∠C = 28°

AC = 17 units

Explanation:

In the given triangle ABC,

m∠B = 90°, Cos(C) =
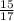`(15)/(17)` and AB = 16 units

Since, Cos(C) =
`\frac{\text{Corresponding side}}{\text{Hypotenuse}}`

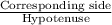
Cos(C) =
`\frac{\text{Corresponding side}}{\text{Hypotenuse}}=(15)/(17)`

`\text{C}=\text{Cos}^(-1)((15)/(17))`

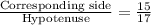
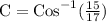
m∠C = 28.07°

m∠C ≈ 28°

Therefore, side BC = 15 units and AC = 17 units

Now we apply Sine rule in the given triangle.

Sin(A) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

=
`\frac{\text{BC}}{\text{AC}}`

=
`(15)/(17)`

A =
`\text{Sin}^(-1)((15)/(17) )`

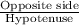
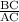
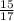
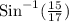
A = 61.93°

m∠A = 62°