Question

Simplify. Can you explain it also?


`\frac{9 {c}^(3) {de}^(2) }{12 {c}^(2)d {e}^(3) }`
​

Answer 1

The answer is

`(3c)/(4e)`

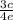
Explanation:

`\frac{9 {c}^(3)d {e}^(2) }{12 {c}^(2) d {e}^(3) }`

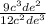
To solve the fraction reduce the fraction with d

That's we have

`\frac{9 {c}^(3) {e}^(2) }{12 {c}^(2) {e}^(3) }`

Next simplify the expression using the rules of indices to simplify the letters in the fraction

For c

Since they are dividing we subtract the exponents

We have

`{c}^(3) / {c}^(2) = {c}^(3 - 2) = c^(1) = c`

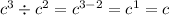
For e

`e^(2) / {e}^(3) = e^(2 - 3) = {e}^( - 1) = (1)/(e)`

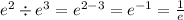
Substituting them into the expression we have

`(9c)/(12e)`

Reduce the fraction by 3

We have the final answer as

`(3c)/(4e)`

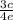
Hope this helps you