Question

A manufacturing company regularly conducts quality control checks at specified periods on the products it manufactures. Historically, the failure rate for LED light bulbs that the company manufactures is 3%. Suppose a random sample of 10 LED light bulbs is selected. What is the probability that

Answer 1

The probability that none of the LED light bulbs are​ defective is 0.7374.

Explanation:

The complete question is:

What is the probability that none of the LED light bulbs are​ defective?

Solution:

Let the random variable X represent the number of defective LED light bulbs.

The probability of a LED light bulb being defective is, P (X) = p = 0.03.

A random sample of n = 10 LED light bulbs is selected.

The event of a specific LED light bulb being defective is independent of the other bulbs.

The random variable X thus follows a Binomial distribution with parameters n = 10 and p = 0.03.

The probability mass function of X is:

`P(X=x)={10\choose x}(0.03)^(x)(1-0.03)^(10-x);\ x=0,1,2,3...`

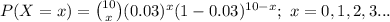
Compute the probability that none of the LED light bulbs are​ defective as follows:

`P(X=0)={10\choose 0}(0.03)^(0)(1-0.03)^(10-0)`

`=1* 1* 0.737424\\=0.737424\\\approx 0.7374`

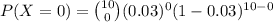
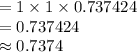
Thus, the probability that none of the LED light bulbs are​ defective is 0.7374.