Answer:
![[Ag^+]=4.82x10^(-5)M](https://img.qammunity.org/2021/formulas/chemistry/college/sqqp20nmgrezmhlnikg8gxr5d6ua95ralx.png)
Step-by-step explanation:
Hello,
In this case, the dissociation reaction for silver phosphate is:
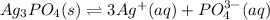
Therefore, the equilibrium expression is:
![Ksp=[Ag^+]^3[PO_4^(3-)]](https://img.qammunity.org/2021/formulas/chemistry/college/72muqevvjdvn7hi9g04i6yottqiff38nog.png)
And in terms of the reaction extent
 is:
is:
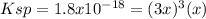
Thus,
 turns out:
turns out:
![1.8x10^(-18)=27x^4\\\\x=\sqrt[4]{(1.8x10^(-18))/(27) } \\\\x=1.61x10^(-5)M](https://img.qammunity.org/2021/formulas/chemistry/college/hrk5bd6cu3wy5x0q65ehtziql54ubfk9y9.png)
In such a way, the concentration of the silver ion is:
![[Ag^+]=3x=3*1.61x10^(-5)M=4.82x10^(-5)M](https://img.qammunity.org/2021/formulas/chemistry/college/c8lxqgc08k1xmpry1tebajcrir70jqjfw9.png)
Best regards.