Question

A plano-convex glass lens of radius of curvature 1.4 m rests on an optically flat glass plate. The arrangement is illuminated from above with monochromatic light of 520-nm wavelength. The indexes of refraction of the lens and plate are 1.6. Determine the radii of the first and second bright fringes in the reflected light.

Answer 1

Given that,

Radius of curvature = 1.4 m

Wavelength = 520 nm

Refraction indexes = 1.6

We know tha,

The condition for constructive interference as,

`t=(m+(1)/(2))(\lambda)/(2)`

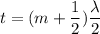
Where,
`\lambda=wavelength`

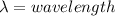
We need to calculate the radius of first bright fringes

Using formula of radius

`r_(1)=√(2tR)`

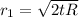
Put the value of t

`r_(1)=\sqrt{2*(m+(1)/(2))(\lambda)/(2)* R}`

Put the value into the formula

`r_(1)=\sqrt{2*(0+(1)/(2))(520*10^(-9))/(2)*1.4}`

`r_(1)=0.603\ mm`

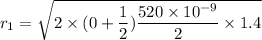
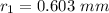
We need to calculate the radius of second bright fringes

Using formula of radius

`r_(2)=\sqrt{2*(m+(1)/(2))(\lambda)/(2)* R}`

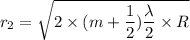
Put the value into the formula

`r_(1)=\sqrt{2*(1+(1)/(2))(520*10^(-9))/(2)*1.4}`

`r_(1)=1.04\ mm`

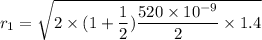
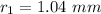
Hence, The radius of first bright fringe is 0.603 mm

The radius of second bright fringe is 1.04 mm.