Given that,
Radius of curvature = 1.4 m
Wavelength = 520 nm
Refraction indexes = 1.6
We know tha,
The condition for constructive interference as,
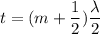
Where,
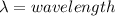
We need to calculate the radius of first bright fringes
Using formula of radius
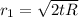
Put the value of t
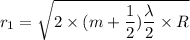
Put the value into the formula
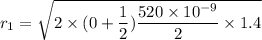
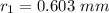
We need to calculate the radius of second bright fringes
Using formula of radius
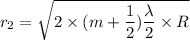
Put the value into the formula
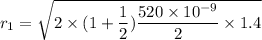
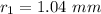
Hence, The radius of first bright fringe is 0.603 mm
The radius of second bright fringe is 1.04 mm.