Question

Air flows through a converging-diverging nozzle/diffuser. A normal shock stands in the diverging section of the nozzle. Assuming isentropic flow, air as an ideal gas, and constant specific heats determine the state at several locations in the system. Solve using equations rather than with the tables.

Answer 1

HELLO your question has some missing parts below are the missing parts

note: The specific heat ratio and gas constant for air are given as k=1.4 and R=0.287 kJ/kg-K respectively.

--Given Values--

Inlet Temperature: T1 (K) = 325

Inlet pressure: P1 (kPa) = 560

Inlet Velocity: V1 (m/s) = 97

Throat Area: A (cm^2) = 5.3

Pressure upstream of (before) shock: Px (kPa) = 207.2

Mach number at exit: M = 0.1

Answer: A) match number at inlet = 0.2683

B) stagnation temperature at inlet = 329.68 k

C) stagnation pressure = 588.73 kPa

D) ) Throat temperature = 274.73 k

Step-by-step explanation:

Determining states at several locations in the system

A) match number at inlet

= V1 / C1 = 97/ 261.427 = 0.2683

C1 = sound velocity at inlet =
`√(K*R*T)` =
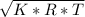`√(1.4 *0.287*10^3)` = 361.427 m/s

v1 = inlet velocity = 97

B) stagnation temperature at inlet

= T1 +
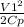`(V1 ^2)/(2Cp)` = 325 +
`(97^2)/(2 * 1.005*10^(-3) )`

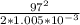
stagnation temperature = 329.68 k

C) stagnation pressure

=
`p1 ( 1 + 0.2Ma^2 )^(3.5)`

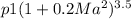
Ma = match number at inlet = 0.2683

p1 = inlet pressure = 560

hence stagnation pressure = 588.73 kPa

D) Throat temperature

=
`(Th)/(T) = (2)/(k+1)`

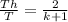
Th = throat temperature

T = stagnation temp at inlet = 329.68 k

k = 1.4

make Th subject of the relation

Th = 329.68 * (2 / 2.4 ) = 274.73 k