Question

COMPUTE

3 ( 2 1/2 - 1 ) + 3/10

Answer 1

`\boxed{ (24)/(5) }`

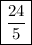
Step-by-step explanation:

`\mathsf{3(2 (1)/(2) - 1) + (3)/(10) }`

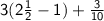
Convert mixed number to improper fraction

`\mathrm{3( (5)/(2) - 1) + (3)/(10) }`

Calculate the difference

⇒
`\mathrm{3( (5 * 1)/(2 * 1) - (1 * 2)/(1 * 2) }) + (3)/(10)`

⇒
`\mathrm{ 3 *( (5)/(2) - (2)/(2)) } + (3)/(10)`

⇒
`\mathrm{3 * ( (5 - 2)/(2) ) + (3)/(10) }`

⇒
`\mathrm{3 * (3)/(2) + (3)/(10) }`

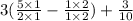
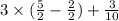
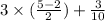
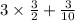
Calculate the product

⇒
`\mathrm{ (3 * 3)/(1 * 2) + (3)/(10) }`

⇒
`\mathrm{ (9)/(2) + (3)/(10)}`

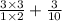
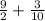
Add the fractions

⇒
`\mathsf{ (9 * 5)/(2 * 5) + (3 * 1)/(10 * 1) }`

⇒
`\mathrm{ (45)/(10) + (3)/(10) }`

⇒
`\mathrm{ (45 + 3)/(10 ) }`

⇒
`\mathrm{ (48)/(10) }`

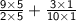
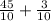
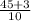
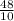
Reduce the numerator and denominator by 2

⇒
`\mathrm{ (24)/(5) }`

Further more Step-by-step explanation:

Addition and Subtraction of like fractions

While performing the addition and subtraction of like fractions, you just have to add or subtract the numerator respectively in which the denominator is retained same.

For example :

Add :
`\mathsf{ (1)/(5) + (3)/(5) = (1 + 3)/(5) } = (4)/(5)`

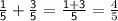
Subtract :
`\mathsf{ (5)/(7) - (4)/(7) = (5 - 4)/(7) = (3)/(7) }`

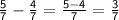
So, sum of like fractions :
`\mathsf{ = (sum \: of \: their \: number)/(common \: denominator) }`

Difference of like fractions :
`\mathsf{ (difference \: of \: their \: numerator)/(common \: denominator) }`

Addition and subtraction of unlike fractions

While performing the addition and subtraction of unlike fractions, you have to express the given fractions into equivalent fractions of common denominator and add or subtract as we do with like fractions. Thus, obtained fractions should be reduced into lowest terms if there are any common on numerator and denominator.

For example:

`\mathsf{add \: (1)/(2) \: and \: (1)/(3) }`

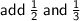
L.C.M of 2 and 3 = 6

So, ⇒
`\mathsf{ (1 * 3)/(2 * 3) + (1 * 2)/(3 * 2) }`

⇒
`\mathsf{ (3)/(6) + (2)/(6) }`

⇒
`(5)/(6)`

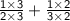
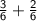
Multiplication of fractions

To multiply one fraction by another, multiply the numerators for the numerator and multiply the denominators for its denominator and reduce the fraction obtained after multiplication into lowest term.

When any number or fraction is divided by a fraction, we multiply the dividend by reciprocal of the divisor. Let's consider a multiplication of a whole number by a fraction:

`\mathsf{4 * (3)/(2) = (4 * 3)/(2) = (12)/(2) = 6}`

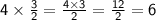
Multiplication for
`\mathsf{ (6)/(5) \: and \: (25)/(3) }` is done by the similar process

`\mathsf{ = (6)/(5) * (25)/(3) = 2 * 5 * 10}`

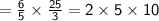
Hope I helped!

Best regards!