Question

The pregnancy length in days for a population of new mothers can be approximated by a normal distribution with a mean of days and a standard deviation of days. ​(a) What is the minimum pregnancy length that can be in the top ​% of pregnancy​ lengths? ​(b) What is the maximum pregnancy length that can be in the bottom ​% of pregnancy​ lengths? ​(a) The minimum pregnancy length is 280 days.

Answer 1

(a) 283 days

(b) 248 days

Explanation:

The complete question is:

The pregnancy length in days for a population of new mothers can be approximated by a normal distribution with a mean of 268 days and a standard deviation of 12 days. ​(a) What is the minimum pregnancy length that can be in the top 11​% of pregnancy​ lengths? ​(b) What is the maximum pregnancy length that can be in the bottom ​5% of pregnancy​ lengths?

Solution:

The random variable X can be defined as the pregnancy length in days.

Then, from the provided information
`X\sim N(\mu=268, \sigma^(2)=12^(2))`.

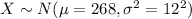(a)

The minimum pregnancy length that can be in the top 11​% of pregnancy​ lengths implies that:

P (X > x) = 0.11

⇒ P (Z > z) = 0.11

⇒ z = 1.23

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\1.23=(x-268)/(12)\\\\x=268+(12* 1.23)\\\\x=282.76\\\\x\approx 283`

Thus, the minimum pregnancy length that can be in the top 11​% of pregnancy​ lengths is 283 days.

(b)

The maximum pregnancy length that can be in the bottom ​5% of pregnancy​ lengths implies that:

P (X < x) = 0.05

⇒ P (Z < z) = 0.05

⇒ z = -1.645

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\\\-1.645=(x-268)/(12)\\\\x=268-(12* 1.645)\\\\x=248.26\\\\x\approx 248`

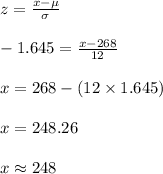
Thus, the maximum pregnancy length that can be in the bottom ​5% of pregnancy​ lengths is 248 days.