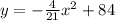Answer:
Explanation:
Because of the nature of the information we are given, we have no choice but to use the equation

and solve for a.
We know by the info that the vertex is (0, 84). We also know that if the vertex is at the origin, and that the base is 42 feet wide, it spans 21 feet to the right of the origin and 21 feet to the left of the origin. That means that we have 2 coordinates from which we need to pick one for our x and y in the equation. I don't like negatives, so I am going to choose the coordinate (21, 0) as x and y. Because this parabola opens upside down, as archways of door openings do, our "a" value better come out algebraically as a negative. Let's see...From the vertex we have that h = 0 and k = 84. So filling in:
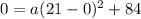 and simplifying a bit:
and simplifying a bit:
0 = 441a + 84 and
-84 = 441a so
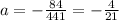 Good, a is negative. Your equation is, then:
Good, a is negative. Your equation is, then: