Question

A simple random sample of 60 households in city 1 is taken. In the sample, there are 45 households that decorate their houses with lights for the holidays. A simple random sample of 50 households is also taken from the neighboring city 2. In the sample, there are 40 households that decorate their houses. What is a 95% confidence interval for the difference in population proportions of households that decorate their houses with lights for the holidays

Answer 1

The calculated value of z = - 0.197 falls in the critical region therefore we reject the null hypothesis and conclude that at the 5% significance level there is significant difference in population proportions of households that decorate their houses with lights for the holidays

Explanation:

We formulate the null and alternative hypotheses as

H0: p1= p2 there is no difference in population proportions of households that decorate their houses with lights for the holidays

against Ha : p1≠ p2 (claim) ( two sided)

The significance level is set at ∝= 0.05

The critical value for two tailed test at alpha=0.05 is ± 1.96

or Z∝= 0.05/2= ± 1.96

The test statistic is

Z = p1-p2/√pq(1/n1 +1/n2)

p1= proportions of households decorating in city 1 = 45/60=0.75

p2= proportions of households decorating in city 2 = 40/50= 0.8

p = the common proportion on the assumption that the two proportion are same.

p =
`(n_1p_1 +n_2p_2)/(n_1+n_2)`

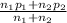
Calculating

p =60 (0.75) + 50 (0.8) / 110

p= 45+ 40/110= 85/110 = 0.772

so q = 1-p= 1- 0.772= 0.227

Putting the values in the test statistic and calculating

z= 0.75- 0.8/ √0.772*0.227( 1/60 + 1/50)

z= -0.05/√ 0.175244 ( 110/300)

z= -0.05/0.25348

z= -0.197

The calculated value of z = - 0.197 falls in the critical region therefore we reject the null hypothesis and conclude that at the 5% significance level there is significant difference in population proportions of households that decorate their houses with lights for the holidays