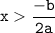Question

Find the intervals on which the function f(x) = ax2 + bx + c (where "a" doesn't = 0) is increasing and decreasing. Describe the reasoning behind your answer.

Answer 1

Explanation:

Given that:

`\mathtt{f(x) = ax^2 + bx + c}`

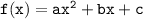
The derivative of the function of x is
`\mathtt{f'(x) = 2ax + b}`

Thus; f(x) is increasing when f'(x) > 0

f(x) is decreasing when f'(x) < 0

i.e

f'(x) > 0 , when b > 0 and a < 0

∴

2ax + b < 0

2ax < - b

`\mathtt{x < (-b)/(2a)}`

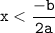
f'(x) < 0 , when b < 0 and a > 0

2ax + b > 0

2ax > - b

`\mathtt{x > (-b)/(2a)}`