Question

A convex refracting surface has a radius of 12 cm. Light is incident in air (n = 1) and refracted into a medium with an index of refraction of 1.5. Light incident parallel to the central axis is focused at a point _____________

Answer 1

36cm from the surface

Step-by-step explanation:

Equation of refraction of a lens is expression according to the formula given below;

`(n_2)/(v) = (n_1)/(u)= (n_2-n_1)/(R)`

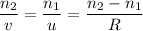
R is the radius of curvature of the convex refracting surface = 12cm

v is the image distance from the refracting surface

u is the object distance from the refracting surface

n₁ and n₂ are the refractive indices of air and the medium respectively

Given parameters

R = 12 cm

u =
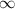`\infty` (since light incident is parallel to the axis)

n₁ = 1

n₂ = 1.5

Required

focus point of the light that is incident and parallel to the central axis (v)

Substituting this values into the given formula we will have;

`(1.5)/(v) - (1)/(\infty)= (1.5-1)/(12)\\\\(1.5)/(v) -0= (0.5)/(12)\\\\(1.5)/(v)= (0.5)/(12)\\\\`

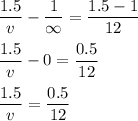
Cross multiply

`1.5*12 = 0.5*v\\ \\18 = 0.5v\\\\v = (18)/(0.5)\\ \\v = 36cm`

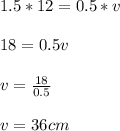
Hence Light incident parallel to the central axis is focused at a point 36cm from the surface