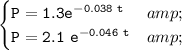Question

Zoologists are studying two newly discovered species of insects in a previously unexplored section of rain forest. They estimate the current population of insect A to be 1.3 million and the current population of insect B to be 2.1 million. As development is encroaching on the section of rain forest where these insects live, the zoologists estimate the populations of insect A to be reducing at a rate of 3.8% and insect B to be reducing at a rate of 4.6%.

Answer 1

A!

Explanation:

Plato

Answer 2

Zoologists are studying two newly discovered species of insects in a previously unexplored section of rain forest. They estimate the current population of insect A to be 1.3 million and the current population of insect B to be 2.1 million. As development is encroaching on the section of rain forest where these insects live, the zoologists estimate the populations of insect A to be reducing at a rate of 3.8% and insect B to be reducing at a rate of 4.6%.

If P represents the population of each species of insect in millions, and t represents the elapsed time in years, then which of the following systems of equations can be used to determine how long it will be before the populations of the two species are equal?

Answer:

the system of equation that can be used to determine how long it will be before the populations of the two species are equal is :

`\begin{cases} {\mathtt{P = 1.3 e^(-0.038 \ t)} & \\ \mathtt{P = 2.1 \ e^(-0.046 \ t)} & \end{cases}`

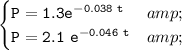
Explanation:

Given that :

the current population of insect A to be 1.3 million

the current population of insect B to be 2.1 million.

As development is encroaching on the section of rain forest where these insects live, the zoologists estimate the populations of insect A to be reducing at a rate of 3.8% and insect B to be reducing at a rate of 4.6%.

The equation that can be used to determine how long it will be before the populations of the two species are equal is an equation for exponential decay, which can be represented as follows:

`\mathtt{y = pe^(-rt)}`

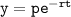
where;

P represents the population of each species of insect in millions

t represents the elapsed time in years

r is the rate of decrease

So, we can have:

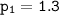`\mathtt{p_1 = 1.3 }` in million and
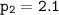`\mathtt{p_2 = 2.1}` in million

Also for rate of decrease;

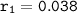`\mathtt{r_1 = 0.038}` and
`\mathtt{r_2 = 0.046}`

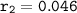
Therefore;

the exponential decay for Population of insect A can now be:

`\mathtt{P = 1.3 e^(-0.038 \ t)}`

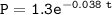
the exponential decay for Population of insect B can now be:

`\mathtt{P = 2.1 \ e^(-0.046 \ t)}`

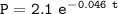
Hence, the system of equation that can be used to determine how long it will be before the populations of the two species are equal is :

`\begin{cases} {\mathtt{P = 1.3 e^(-0.038 \ t)} & \\ \mathtt{P = 2.1 \ e^(-0.046 \ t)} & \end{cases}`