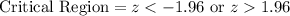Question

wo independent samples have been selected, 100 observations from population 1 and 76 observations from population 2. The sample means have been calculated to be x⎯⎯⎯1=11.9 and x⎯⎯⎯2=12.9. From previous experience with these populations, it is known that the variances are σ21=27 and σ22=23. (a) Determine the rejection region for the test of

Answer 1

`\text{Critical Region} = z<-1.96\ \text{or}\ z>1.96`

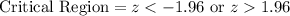
Explanation:

A test for the difference between two population means is to be performed.

As the population variances are known, the z-test will be used.

The hypothesis can be defined as follows:

H₀: μ₁ = μ₂ vs. Hₐ: μ₁ ≠ μ₂

Assume that the significance level of the test is, α = 0.05.

The critical region can be defined as follows:

The critical value of z for α = 0.05 is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025) =-1.96\\\\z_(1-\alpha/2)=z_(1-0.05/2)=z_(0.975) =1.96`

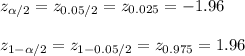
Use a z-table.

`\text{Critical Region} = z<-1.96\ \text{or}\ z>1.96`