Question

A research center claims that ​% of adults in a certain country would travel into space on a commercial flight if they could afford it. In a random sample of adults in that​ country, ​% say that they would travel into space on a commercial flight if they could afford it. At ​, is there enough evidence to reject the research

Answer 1

Complete Question

A research center claims that ​30% of adults in a certain country would travel into space on a commercial flight if they could afford it. In a random sample of 700 adults in that​ country, ​34% say that they would travel into space on a commercial flight if they could afford it. At ​, is there enough evidence to reject the research center's claim

Answer:

Yes there is sufficient evidence to reject the research center's claim.

Explanation:

From the question we are told that

The population proportion is p = 0.30

The sample proportion is
`\r p = 0.34`

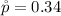
The sample size is n = 700

The null hypothesis is
`H_o : p = 0.30`

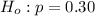
The alternative hypothesis is
`H_a : p \\e 0.30`

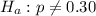
Here we are going to be making use of level of significance = 0.05 to carry out this test

Now we will obtain the critical value of
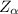`Z_(\alpha )` from the normal distribution table , the value is
`Z_(\alpha ) = 1.645`

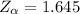
Generally the test statistics is mathematically represented as

`t = \frac{ \r p - p }{ \sqrt{ ( p (1-p))/(n) } }`

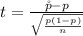
substituting values

`t = \frac{ 0.34 - 0.30 }{ \sqrt{ ( 0.30 (1-0.30 ))/( 700) } }`

`t = 2.31`

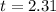
Looking at the values of t and
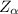`Z_(\alpha )` we see that
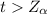`t > Z_(\alpha )` hence the null hypothesis is rejected

Thus we can conclude that there is sufficient evidence to reject the research center's claim.