Question

The number of daylight hours, D, in the city of Worcester, Massachusetts, where x is the number of days after January 1 (), may be calculated by the function: What is the period of this function? N/A What is the amplitude of this function? 12 What is the horizontal shift? What is the phase shift? What is the vertical shift? How many hours of sunlight will there be on February 21st of any year?

Answer 1

a. 365; b. 3; c. 78; d. 1.343 rad; e. 12; f. 10.66

Step-by-step explanation:

Assume that the function is

`D(x) = 3 \sin \left ((2\pi)/(365)(x - 78) \right ) + 12`

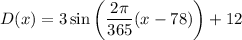
The general formula for a sinusoidal function is

y = A sin(B(x - C))+ D

|A| = amplitude

B = frequency

2π/B = period, P

C = horizontal shift (phase shift)

D = vertical shift

By comparing the two formulas, we find

|A| = 3

B = 2π/365

C = 78

D = 12

a. Period

P = 2π/B = 2π/(2π/365) = 2π × 365/2π = 365

The period is 365.

b. Amplitude

|A| = 3

The amplitude is 3.

c. Horizontal shift

C= 78

The horizontal shift is 78.

d. Phase shift (φ)

Ths phase shift is the horizontal shift expressed in radians.

φ = C × 2π/365 = 78 × 2π/365 ≈ 1.343

The phase shift is 1.343 rad.

e. Vertical shift

D = 12

The vertical shift is 12.

f. Hours of sunlight on Feb 21

Feb 21 is the 52nd day of the year, so x = 51 (the number of days after Jan 1),

`\begin{array}{rcl}D(x) &=& 3 \sin \left ((2\pi)/(365)(x - 78) \right ) + 12\\\\&=& 3 \sin (0.01721(51 - 78) ) + 12\\&=& 3\sin(-0.4648) + 12\\&=& 3(-0.4482) + 12\\\&=& -1.345 + 12\\& = & \textbf{10.66 h}\\\end{array}`

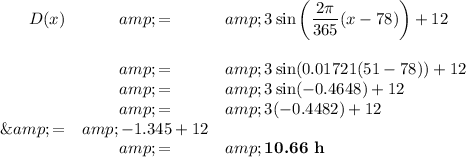
There will be 10.66 h of sunlight on Feb 21 of any given year.

The figure below shows the graph of the function from 0 ≤ x ≤ 365.