Question

A television screen has a length to width ratio of 8 to 5 and a perimeter of 117 inches. What is the diagonal measure of the screen (to the nearest tenth of an inch)?

Answer 1

`D = 42.5\ inch`

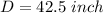
Explanation:

Given

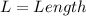`L = Length` and
`W = Width`

`L:W = 8: 5`

`Perimeter = 117`

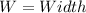
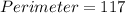
Required

Determine the Diagonal

First, the dimension of the screen has to be calculated;

Recall that;
`L:W = 8: 5`

Convert to division

`(L)/(W) = (8)/(5)`

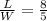
Multiply both sides by W

`W * (L)/(W) = (8)/(5) * W`

`L = (8W)/(5)`

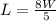
The perimeter of a rectangle:

`Perimeter = 2(L+W)`

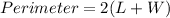
Substitute
`L = (8W)/(5)`

`Perimeter = 2((8W)/(5)+W)`

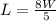
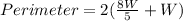
Take LCM

`Perimeter = 2((8W + 5W)/(5))`

`Perimeter = 2((13W)/(5))`

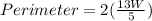
Substitute 117 for Perimeter

`117 = 2((13W)/(5))`

`117 = (26W)/(5)`

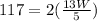
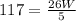
Multiply both sides by
`(5)/(26)`

`(5)/(26) * 117 = (26W)/(5) * (5)/(26)`

`(5 * 117)/(26) = W`

`(585)/(26) = W`

`22.5 = W`

`W = 22.5`

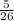
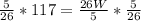
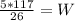
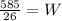
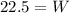
Recall that

`L = (8W)/(5)`

`L = (8 * 22.5)/(5)`

`L = (180)/(5)`

`L = 36`

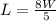
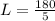
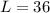
The diagonal of a rectangle is calculated using Pythagoras theorem as thus;

`D = √(L^2 + W^2)`

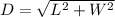
Substitute values for L and W

`D = √(36^2 + 22.5^2)`

`D = √(1296 + 506.25)`

`D = √(1802.25)`

`D = √(1802.25)`

`D = 42.4529150943`

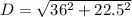
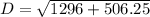
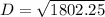
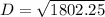
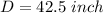`D = 42.5\ inch` (Approximated)