Answer:
Explanation:
Hello, first, let's use the product rule.
Derivative of uv is u'v + u v', so it gives:
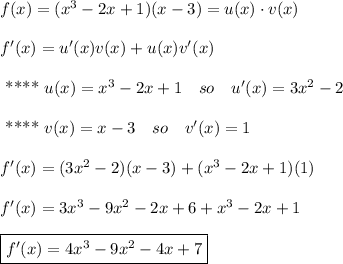
Now, we distribute the expression of f(x) and find the derivative afterwards.
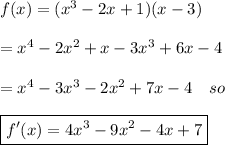
Hope this helps.
Do not hesitate if you need further explanation.
Thank you