Question

Find the derivative of the function f(x) = (x3 - 2x + 1)(x – 3) using the product rule.

then by distributing and make sure they are the same answer ​

Answer 1

Explanation:

Hello, first, let's use the product rule.

Derivative of uv is u'v + u v', so it gives:

`f(x)=(x^3-2x+1)(x-3)=u(x) \cdot v(x)\\\\f'(x)=u'(x)v(x)+u(x)v'(x)\\\\ \text{ **** } u(x)=x^3-2x+1 \ \ \ so \ \ \ u'(x)=3x^2-2\\\\\text{ **** } v(x)=x-3 \ \ \ so \ \ \ v'(x)=1\\\\f'(x)=(3x^2-2)(x-3)+(x^3-2x+1)(1)\\\\f'(x)=3x^3-9x^2-2x+6 + x^3-2x+1\\\\\boxed{f'(x)=4x^3-9x^2-4x+7}`

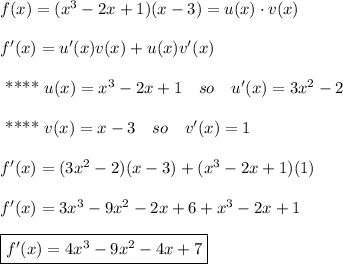
Now, we distribute the expression of f(x) and find the derivative afterwards.

`f(x)=(x^3-2x+1)(x-3)\\\\=x^4-2x^2+x-3x^3+6x-4\\\\=x^4-3x^3-2x^2+7x-4 \ \ \ so\\ \\\boxed{f'(x)=4x^3-9x^2-4x+7}`

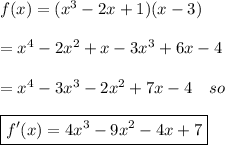
Hope this helps.

Do not hesitate if you need further explanation.

Thank you