Question

What is the slope of the line that passes through (2, 12) and (4, 20)?On the graph of the equation 3x + 2y = 18, what is the value of the y-intercept?

Answer 1

Answer: The slope of the line that passes through (2, 12) and (4, 20) is 4.

The value of the y-intercept is 9.

Explanation:

Slope of line passing through (a,b) and (c,d) =
`(d-b)/(c-a)`

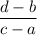
Then, the slope of the line that passes through (2, 12) and (4, 20) =
`(20-12)/(4-2)`

`=(8)/(2)=4`

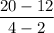
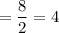
So, the slope of the line that passes through (2, 12) and (4, 20) is 4.

To find the y-intercept of 3x + 2y = 18, first write in slope intercept form y=mx+c ( where c= y-intercept ).

`2y=-3x+18\\\\\Rightarrow\ y=-(3)/(2)x+9`

By comparison, c= 9

Hence, the value of the y-intercept is 9.