Question

A man lends 12,500 at 12% for the first

year, at 15% for the second year and at 18%
for the third year. If the rates of interest are
compounded yearly; find the difference
between the C.I. of the first year and the
compound interest for the third year.​

Answer 1

Answer: $1398

Explanation:

Given , Principal (P) = $12,500

Rate of interest for 1st year
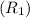`(R_1)`= 12% =0.12

Rate of interest for 2nd year
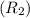`(R_2)`= 15% =0.15

Rate of interest for 3rd year
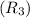`(R_3)`= 18% =0.18

Interest for first year =
`I=P* R_1* T`

=
`12500* 0.12* 1`

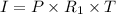
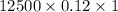
= $1500

Now, For second year new principal
`P_2 = \$12,500+\$1,500 =\$14,000`

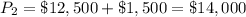
Interest for second year =
`I=P_2* R_2* T`

=
`14000* 0.15* 1`

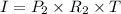
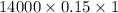
= $2100

Now, For third year new principal
`P_3 = \$14000+\$2,100 =\$16,100`

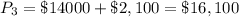
Interest for third year =
`I=P_3* R_3* T`

=
`16100* 0.18* 1`

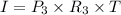
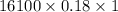
= $2898

Difference between the compound interest of the first year and the compound interest for the third year. = $2898 - $1500 = $1398

Hence, the difference between the compound interest of the first year and the compound interest for the third year is $1398 .