Question

A survey showed that among 785 randomly selected subjects who completed four years of college, 144 of them are smokers and 84 do not smoke (based on data from the American Medical Association). Suppose you want to test at the 0.01 significance level the claim that the rate of smoking among those with four years of college is less than the 27% rate for the general population.

A. State the null and alternative hypotheses.
B. Find the sample statistic and the p-value.
C. What is your conclusion?

Answer 1

We conclude that the rate of smoking among those with four years of college is less than the 27% rate for the general population.

Explanation:

We are given that a survey showed that among 785 randomly selected subjects who completed four years of college, 144 of them are smokers.

Let p = population proportion of smokers among those with four years of college

So, Null Hypothesis,
`H_0` : p
`\geq` 27% {means that the rate of smoking among those with four years of college is more than or equal to the 27% rate for the general population}

Alternate Hypothesis,
`H_A` : p < 27% {means that the rate of smoking among those with four years of college is less than the 27% rate for the general population}

The test statistics that will be used here is One-sample z-test for proportions;

T.S. =
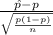`\frac{\hat p-p}{\sqrt{(p(1-p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of smokers =
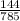`(144)/(785)` = 0.18

n = sample of subjects = 785

So, the test statistics =
`\frac{0.18-0.27}{\sqrt{(0.27(1-0.27))/(785) } }`

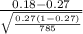
= -5.68

The value of z-test statistics is -5.68.

Also, the P-value of the test statistics is given by;

P-value = P(Z < -5.68) = Less than 0.0001

Now, at a 0.01 level of significance, the z table gives a critical value of -2.3262 for the left-tailed test.

Since the value of our test statistics is less than the critical value of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the rate of smoking among those with four years of college is less than the 27% rate for the general population.