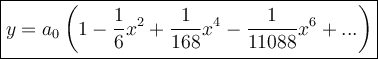
Hello, please consider the following.
The equation is
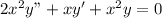
Assume that, on a given domain where the sum is defined,
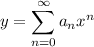
is a solution of the equation and we will find a recursion formula for the
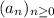 , then
, then
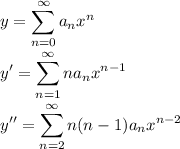
So the equation becomes
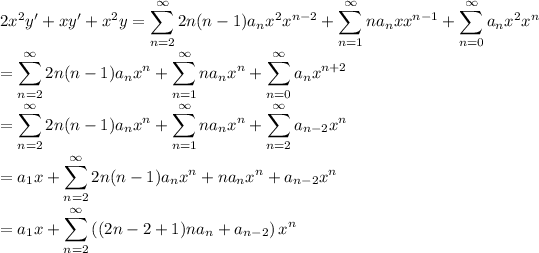
And this is equal to 0, so we can say that
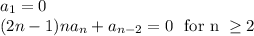
It comes
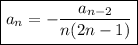
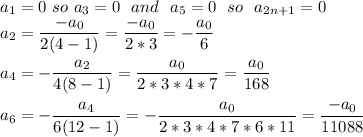
So
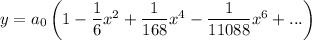
We can go further to find a generic expression but only 3 non-zero terms were requested.
Hope this helps.
Do not hesitate if you need further explanation.
Thank you