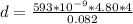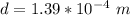Question

Two narrow slits are illuminated by a laser with a wavelength of 593 nm. The interference pattern on a screen located x = 4.80 m away shows that the fourth-order bright fringe is located y = 8.20 cm away from the central bright fringe. Calculate the distance between the two slits.

Answer 1

The distance is
`d = 1.39 *10^(-4) \ m`

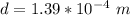
Step-by-step explanation:

From the question we are told that

The wavelength is
`\lambda = 593 \ nm = 593 *10^(-9) \ m`

The distance of the screen is x = 4.80 m

The location of the fourth order bright fringe is y = 8.20 cm = 0.082 m

The order of the fringe is n = 4

Generally the position of a fringe with respect to the central fringe is mathematically represented as

`y = ( n * x * \lambda )/(d)`

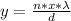
Where d is the distance between the slits, so making d the subject

`d = (\lambda * x * n )/( y )`

substituting values

`d = ( 593 *10^(-9) * 4.80 * 4 )/( 0.082 )`

`d = 1.39 *10^(-4) \ m`