Question

Test the claim that the proportion of people who own cats is significantly different than 80% at the 0.2 significance level. The null and alternative hypothesis would be:______.

A. H0 : μ = 0.8 H 1 : μ ≠ 0.8
B. H0 : p ≤ 0.8 H 1 : p > 0.8
C. H0 : p = 0.8 H 1 : p ≠ 0.8
D. H0 : μ ≤ 0.8 H 1 : μ > 0.8
E. H0 : p ≥ 0.8 H 1 : p < 0.8
F. H0 : μ ≥ 0.8 H 1 : μ < 0.8
The test is:_____.
a. left-tailed
b. right-tailed
c. two-tailed
Based on a sample of 200 people, 79% owned cats.
The test statistic is:______.
The p-value is:_____.
Based on this we:_____.
A. Fail to reject the null hypothesis.
B. Reject the null hypothesis.

Answer 1

C. H0 : p = 0.8 H 1 : p ≠ 0.8

The test is:_____.

c. two-tailed

The test statistic is:______p ± z (base alpha by 2)
`\sqrt{(pq)/(n) }`

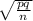
The p-value is:_____. 0.09887

Based on this we:_____.

B. Reject the null hypothesis.

Explanation:

We formulate null and alternative hypotheses as proportion of people who own cats is significantly different than 80%.

H0 : p = 0.8 H 1 : p ≠ 0.8

The alternative hypothesis H1 is that the 80% of the proportion is different and null hypothesis is , it is same.

For a two tailed test for significance level = 0.2 we have critical value ± 1.28.

We have alpha equal to 0.2 for a two tailed test . We divided alpha with 2 to get the answer for a two tailed test. When divided by two it gives 0.1 and the corresponding value is ± 1.28

The test statistic is

p ± z (base alpha by 2)
`\sqrt{(pq)/(n) }`

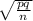
Where p = 0.8 , q = 1-p= 1-0.8= 0.2

n= 200

Putting the values

0.8 ± 1.28
`\sqrt{(0.8*0.2)/(200) }`

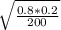
0.8 ± 0.03620

0.8362, 0.7638

As the calculated value of z lies within the critical region we reject the null hypothesis.