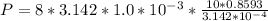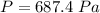Question

Water flows at 0.00027 m3/s through a 10-m long garden hose lying on the ground, with a radius of 0.01 m. Water has a viscosity of 1 mPa.s What is the magnitude of gauge pressure in Pa of the water entering the hose

Answer 1

The gauge pressure is
`P = 687.4 \ Pa`

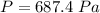
Step-by-step explanation:

From the question we are told that

The rate of flow is
`Q = 0.00027 m^3 /s`

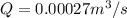
The height is h = 10 m

The radius is r = 0.01 m

The viscosity is
`\eta = 1mPa \cdot s = 1 *10^(-3) \ Pa\cdot s`

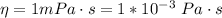
Generally the gauge pressure according to Poiseuille's equation is mathematically represented as

`P = 8 \pi \eta * (L * v )/( A)`

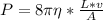
Here v is the velocity of the water which is mathematically represented according to continuity equation as

`v = (Q)/(A )`

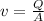
Where A is the cross-sectional area which is mathematically represented as

`A = \pi r^2`

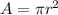
substituting values

`A = 3.142 *(0.01)^2`

`A = 3.142 *10^(-4) \ m^2`

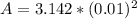
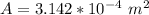
So

`v = ( 0.00027)/(3.142*10^(-4))`

`v = 0.8593 \ m/s`

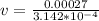
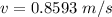
So

`P = 8 * 3.142 * 1.0*10^(-3)* (10 * 0.8593 )/( 3.142*10^(-4))`

`P = 687.4 \ Pa`