Answer:
![$\[x^2 + 22x + 121\]$](https://img.qammunity.org/2021/formulas/mathematics/middle-school/h3ue8164kn3nqer30tjzqpzlpitbot3b4l.png)
Explanation:
Given
![$\[x^2 + 22x + \underline{~~~~}.\]$](https://img.qammunity.org/2021/formulas/mathematics/middle-school/upbdomua2as4ohwi27r4gx5v71fmp0ru9f.png)
Required
Fill in the gap
Represent the blank with k
![$\[x^2 + 22x + k\]$](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xdx8v7xdjjcsyrw4vwi6kre2jicvwy0lf0.png)
Solving for k...
To do this, we start by getting the coefficient of x
Coefficient of x = 22
Divide the coefficient by 2
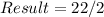
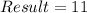
Take the square of this result, to give k
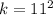
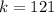
Substitute 121 for k
![$\[x^2 + 22x + 121\]$](https://img.qammunity.org/2021/formulas/mathematics/middle-school/h3ue8164kn3nqer30tjzqpzlpitbot3b4l.png)
The expression can be factorized as follows;
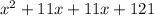
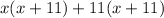
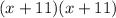
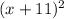
Hence, the quadratic expression is
![$\[x^2 + 22x + 121\]$](https://img.qammunity.org/2021/formulas/mathematics/middle-school/h3ue8164kn3nqer30tjzqpzlpitbot3b4l.png)