Question

I need help please, I am so confused.​

Answer 1

`\begin{tabular}\cline{1-3} Equation & x-intercepts & x-coordinate of vertex\\\cline{1-3} $y=x(x-2)$ & $x=0, x=2$ & $x=1$\\\cline{1-3} $y=(x-4)(x+5)$ & $x=-5, x=4$ & $x=-0.5$\\\cline{1-3} $y=-5x(x-3)$ & $x=0, x=3$ & $x=1.5$\\\cline{1-3} \end{tabular}`

Explanation:

x-intercepts are when the curve intercepts the x-axis, so when y =0.

Therefore, to find the x-intercepts, substitute y = 0 and solve for x.

The vertex is the turning point: the minimum point of a parabola that opens upward, and the maximum point of the parabola that opens downward. As a parabola is symmetrical, the x-coordinate of the vertex is the midpoint of the x-intercepts.

Equation:
`y=x(x-2)`

`\implies x(x-2)=0`

`\implies x=0`

`\implies (x-2)=0 \implies x=2`

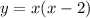
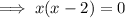
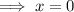
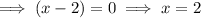
Therefore, the x-intercepts are x = 0 and x = 2

The midpoint of the x-intercepts is x = 1, so the x-coordinate of the vertex is x = 1

Equation:
`y=(x-4)(x+5)`

`\implies (x-4)(x+5)=0`

`\implies (x-4)=0 \implies x=4`

`\implies (x+5)=0 \implies x=-5`

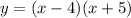
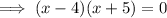
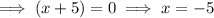
Therefore, the x-intercepts are x = -5 and x = 4

The midpoint of the x-intercepts is x = -0.5, so the x-coordinate of the vertex is x = -0.5

Equation:
`y=-5x(3-x)`

`\implies -5x(3-x)=0`

`\implies -5x=0 \implies x=0`

`\implies (3-x)=0 \implies x=3`

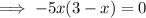
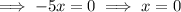
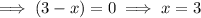
Therefore, the x-intercepts are x = 0 and x = 3

The midpoint of the x-intercepts is x = 1.5, so the x-coordinate of the vertex is x = 1.5

`\begin{tabular}\cline{1-3} Equation & x-intercepts & x-coordinate of vertex\\\cline{1-3} $y=x(x-2)$ & $x=0, x=2$ & $x=1$\\\cline{1-3} $y=(x-4)(x+5)$ & $x=-5, x=4$ & $x=-0.5$\\\cline{1-3} $y=-5x(x-3)$ & $x=0, x=3$ & $x=1.5$\\\cline{1-3} \end{tabular}`