Question

In trapezoid ABCD, AB ∥ CD , m∠A=90°, AD=8 in, DC=9 in, CB=10 in, and ∠B is acute. Find DB.

Answer 1

The answer to this question is that the length of DB is 17 in

Answer 2

the length of DB is 17 in

Explanation:

Consider the sketch attached.

We will draw an imaginary line from point C to met line AB at point E.

A right-angled triangle will now be formed between points CBE.

The dimensions of the right-angled triangle will be:

CB = 10 in

CE= 8 in

EB = unknown

We will now proceed to find out the length of side EB using the Pythagoras' theorem.

`EB =√(CB^2 -CE^2) \\EB =√(10^2 -8^2) \\EB = 6 in`

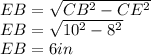
From the shape, we can find out that another right-angled triangle is made between points DAB.

The dimensions of the triangle are:

DA= 8in

AB = 9 in + 6 in = 15 in

DB = unknown.

We will now proceed to find out the length of side DB using the Pythagoras' theorem.

`DB =√(AD^2 +AB^2) \\DB =√(8^2 +15^2) \\DB = 17 in`

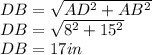
Therefore, the length of DB is 17 in