Question

Please help with this

Answer 1

`\sin \left(\theta \right)-(1)/(2)\cos \left(2\theta \rightt)+C`

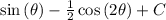
Explanation:

We are given the graph of r = cos( θ ) + sin( 2θ ) so that we are being asked to determine the integral. Remember that
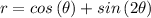`\:r=cos\left(\theta \right)+sin\left(2\theta \right)` can also be rewritten as
`\int \cos \left(\theta \right)+\sin \left(2\theta \right)d\theta \right`.

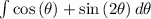Let's apply the functional rule
`\int f\left(x\right)\pm g\left(x\right)dx=\int f\left(x\right)dx\pm \int g\left(x\right)dx`,

`\int \cos \left(\theta \right)+\sin \left(2\theta \right)d\theta \right` =
`\int \cos \left(\theta \right)d\theta \right+\int \sin \left(2\theta \right)d\theta \right`

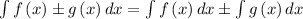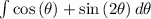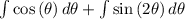
At the same time
`\int \cos \left(\theta \right)d\theta \right=\sin \left(\theta \right)` =
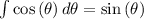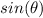`sin( \theta \right ))`, and
`\int \sin \left(2\theta \right)d\theta \right` =
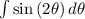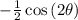`-(1)/(2)\cos \left(2\theta \right)`. Let's substitute,

`\int \cos \left(\theta \right)d\theta \right+\int \sin \left(2\theta \right)d\theta \right` =
`\sin \left(\theta \right)-(1)/(2)\cos \left(2\theta \right)`

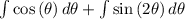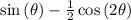
And adding a constant C, we receive our final solution.

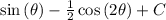`\sin \left(\theta \right)-(1)/(2)\cos \left(2\theta \rightt)+C` - this is our integral