Answer:
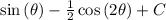
Explanation:
We are given the graph of r = cos( θ ) + sin( 2θ ) so that we are being asked to determine the integral. Remember that
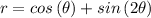 can also be rewritten as
can also be rewritten as
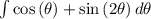 .
.
Let's apply the functional rule
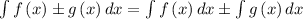 ,
,
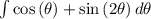 =
=
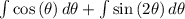
At the same time
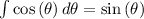 =
=
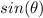 , and
, and
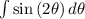 =
=
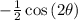 . Let's substitute,
. Let's substitute,
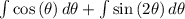 =
=
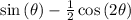
And adding a constant C, we receive our final solution.
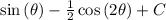 - this is our integral
- this is our integral