Question

Suppose that three computer boards in a production run of forty are defective. A sample of five is to be selected to be checked for defects.

a. How many different samples can be chosen?
b. How many samples will contain at least one defective board?
c. What is the probability that a randomly chosen sample of five contains at least one defective board?

Answer 1

(a) 658,008 different samples can be chosen.

(b) 222,111 samples will contain at least one defective board.

(c) The probability that a randomly chosen sample of five contains at least one defective board is 0.34.

Explanation:

We are given that three computer boards in a production run of forty are defective. A sample of five is to be selected to be checked for defects.

(a) To find how many different samples can be chosen, we will use a combination formula here because the order of selecting a sample of 5 from the production run of 40 doesn't matter.

Here, n = total sample = 40 and r = selected sample = 5

So, the combination formula is;
`^(n)C_r= (n!)/(r! * (n-r)!)`

`^(40)C_5= (40!)/(5! * (40-5)!)`

`^(40)C_5= (40!)/(5! * 35!)`

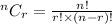
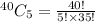
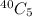`^(40)C_5` = 658,008 ways

So, 658,008 different samples can be chosen.

(b) To find how many samples will contain at least one defective board, we will first find how many samples will contain no or 0 defective board.

For this also, we will use a combination where n = 40 - 3 = 37 non-defective computer board and a sample of r = 5 computer boards.

So,
`^(n)C_r= (n!)/(r! * (n-r)!)`

`^(37)C_5= (37!)/(5! * (37-5)!)`

`^(37)C_5= (37!)/(5! * 32!)`

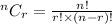
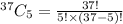
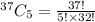
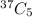`^(37)C_5` = 435,897 ways

This means that 435,897 of the 658,008 samples will contain no defective board.

Now, the samples that will contain at least one defective board = Total samples - Samples that contain no defective board

= 658,008- 435, 897

= 222,111

(c) The probability that a randomly chosen sample of five contains at least one defective board is given by;

Required Probability =
`(222,111)/(658,008)`

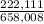
= 0.34 or 34%